疑似3D 2
画像を使って
クォータービューとは違って遠近法に基づいて近くなら大きく、遠くなら小さく見えるようにするにはどうしたらいいでしょう?
今回は少し本格的な3Dの計算をしていきます。といっても基礎的な考え方だけです。私も深くは知りません。
ぶっちゃけ3Dを本気でやりたいなら Unity とか Unreal Engine をおすすめします。物理演算やら何やらも手軽にできるのでコードを書かなくてもある程度作れるみたいです。
まあでも知っておいて損はないと思います。興味がなければ「そんなこともできるのね」くらいで構いません。
では「ThreeDimension」クラスを作成してください。
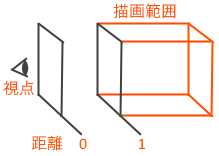
3D空間を考えたとき、今までと違って描画領域の決まった座標はありません。もちろん最終的には座標を指定して描画はしますがそれはどこから見ているか視点によって変わってくるので3D空間の座標は大きくても小さくても問題は無いということです。
例えば幅・高さ・奥行が 50000×50000×100000 でも 5×5×10 でも比率は 1:1:2 で同じなので同じ空間だと考えていいでしょう。これは扱いやすい大きさで構いません。幅と高さを描画領域に合わせて倍率を変えれば描画できます。
距離による見た目の大きさは距離に反比例します。大きさが10として距離が1なら 10/1=10、距離が100なら 10/100=0.1 です。これが一番大事です。これがわかればもうこの先は読む必要ありません。…いや言い過ぎましたがこの法則を使って計算していくだけです。
いつもの描画セットでいきます。画像は以前使ったものをまた使うので新たに用意する必要はありません。
距離が 5~0.05 までを定速でループさせます。奥行は z で横縦が x, y にします。x, y は今までの座標のように左上が(0, 0)とするのが考えやすいです。この(0, 0)は描画領域の(0, 0)とは違います。3D空間の座標系です。
遠くにいるときはなかなか近づいてくるようにみえませんが近くに来たら一瞬で大きくなっていきます。これが距離による見た目の大きさです。
画像サイズ 32 を z で割っているだけです。z で割るので距離が0のときは計算できません。マイナスのときもおかしなことになるので z は常に正になるようにしてください。
近くに来たときに大きくなり過ぎると思ったら描画する距離を調整します。今は視点からほぼ0距離で描画しています。視点からの距離を 1 にすれば元の画像サイズの等倍までしか拡大されません。つまり距離が 1 より近くなったら描画しないようにします。
z = (z - 0.05 < 1) ? 5 : z - 0.05;こうですね。試してみてください。
せっかく3Dにするなら近くに迫ったときは大きく描画したいですから視点からの距離はあまり遠ざけないようにするか遠ざけるなら大きい画像を使うか元のサイズより拡大して使いたいところです。
次は x, y をランダムにして定速で近づいてくるようにしてみましょう。上に出現したら近づいてくるほど上に見えるようにします。下なら下、左右も同じです。
これを考えるには先ほどより明確に描画する範囲を決めなければなりません。
3D空間の一番奥と手前が2Dの座標のどこにくるかわからないと描画できません。
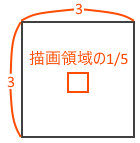
まず3D空間の大きさから決めていきましょう。これは(x, y, z)が(3, 3, 5)にしましょう。これはあくまで目安です。どの範囲を描画するかによって変わるのでそれほど意味はありません。
一番手前は x, y の大きさにします。2Dの描画領域にすっぽりはまる大きさというわけです。これが一番簡単でわかりやすいです。
一番奥は画面の中央にします。これも中央が一番計算しやすいです。距離が 5 ですから 描画領域の 1/5 の大きさで矩形を考えます。この 1/5 の矩形は手前の描画領域をそのまま奥まで平行移動したものです。奥へいくほど3D空間の x, y の範囲はより広く描画領域に入ってくるので一番奥では(x, y)=(15, 15)の範囲が視界に入ることになります。
3D空間での画像の x, y 座標は画像の中心にします。出現時に 0~3 のランダムにします。
ここでおもむろに3D空間の座標をずらします。x, y は画面の中央を(0, 0)にします。x は右でプラス、左でマイナスなのは変わりません。y も同じです。
距離が 1 のときを基準にしたいと思います。距離が 1 のときに(3, 3)の範囲が描画領域と同じになるようにします。このときの画像の大きさが3D空間で 1 になるようにします。
これで必要なものは揃いました。計算していきましょう。
描画の座標 dx はまず3D空間の中央が 0 ですから基準は AREA_X / 2 になります。ここに x を加算していきますが奥行によるずれも考慮します。
こういうときはわかりやすい値を決めて計算するのが無難です。x が左端にいるときは -1.5 です。距離が 1 のときに描画領域の左端にいてほしい。
となると描画領域の中央は 250 ですから左端なら -1.5 * ??? / 1 = -250 となる ??? を知りたい。中央が 0 なので左端は -250 です。この ??? は AREA_X / 3.0 です。
なぜそうなるのかというと、3D空間は(3, 3, 5)と決めたからです。3D空間の 3 は2D座標の AREA_X と同じ意味です。 AREA_X / 3.0 は3D空間で x が 1 動いたときの2D座標での動きです。割合の計算ですね。
一番奥の左端にいるときは -1.5 * AREA_X / 3.0 / 5 = -50 となります。一番奥ですから奥行は 5 です。そして2D座標の中央から -50 ですね。右端なら +50 になります。
この説明でわかってもらえるか不安ですが、3D空間の座標を2Dに変換しています。
コードにしていきます。
画像サイズは距離が 1 のときに 1 になりますから3D空間の 1 は2Dだと AREA_X / 3.0 です。
どうでしょう?楽しめなくなってきましたか?
頭の中で1つ1つをしっかりイメージできればそれほど難しいわけではありません。描画する座標は中央を基準に x * 2Dの範囲 / 3Dの範囲 / z を加算しているだけです。
この「2Dの範囲 / 3Dの範囲 / z」で座標を変換しています。
とはいえ、私も久し振りに計算したので少し悩みました笑。
ここまでやっといてなんですが、疑似3Dはあまり使い道はありません!!!
というのも Java だと画像を動的に変形できないみたいなんですよね。変形とは元々矩形の画像を台形にしたり平行四辺形にしたりということです。DirectX ならそういう関数もありましたが Java は無いみたいです。静的に変形する方法はあるんですけどね。多分処理に時間がかかるので1フレームごとにたくさん変形させるゲームには使えません。ライブラリを探せばもしかしたら見つかるかもしれません。
変形できないと何が不便かというと、奥行のあるものはすべて変形するからです。
ここまでのコードでは奥行のある表現はしていますが画像に奥行はなく1枚の画像でしかありません。
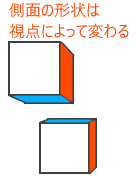
例えば立方体を思い浮かべてください。今回のコードでは立方体の正面だけを描画したに過ぎません。側面を描画しようとすると縦横の揃った矩形では無理です。側面は視点によって形を変えますので事前に画像を用意することもできません。
といった理由で、それでも3Dを使いたいなら奥行を描画しないものにします。空とか宇宙なら地形などの奥行を表現しなくても大丈夫です。他には3Dダンジョンのように壁や床の位置が決まっているなら変形しなくても描画できるのであらかじめ変形している画像を何パターンか用意すればできると思います。2Dしかなかった昔のゲームでもそういった工夫をしています。
PHANTASY STAR は今でも続編が出たりしているようですが最初期は 1987年です。このゲームでダンジョンがぬるぬる動いているのを見て「すげーっ!」って興奮していましたね。おそらく今回のコードのような計算ではなく動いているところを全部画像にしたのではないかと思います。
工夫次第ではいけなくもないといった感じです。
今回は少し本格的な3Dの計算をしていきます。といっても基礎的な考え方だけです。私も深くは知りません。
ぶっちゃけ3Dを本気でやりたいなら Unity とか Unreal Engine をおすすめします。物理演算やら何やらも手軽にできるのでコードを書かなくてもある程度作れるみたいです。
まあでも知っておいて損はないと思います。興味がなければ「そんなこともできるのね」くらいで構いません。
では「ThreeDimension」クラスを作成してください。
3D空間を考えたとき、今までと違って描画領域の決まった座標はありません。もちろん最終的には座標を指定して描画はしますがそれはどこから見ているか視点によって変わってくるので3D空間の座標は大きくても小さくても問題は無いということです。
例えば幅・高さ・奥行が 50000×50000×100000 でも 5×5×10 でも比率は 1:1:2 で同じなので同じ空間だと考えていいでしょう。これは扱いやすい大きさで構いません。幅と高さを描画領域に合わせて倍率を変えれば描画できます。
距離による見た目の大きさは距離に反比例します。大きさが10として距離が1なら 10/1=10、距離が100なら 10/100=0.1 です。これが一番大事です。これがわかればもうこの先は読む必要ありません。…いや言い過ぎましたがこの法則を使って計算していくだけです。
いつもの描画セットでいきます。画像は以前使ったものをまた使うので新たに用意する必要はありません。
ThreeDimension.java
package application;
import java.awt.BasicStroke;
import java.awt.Color;
import java.awt.Font;
import java.awt.Graphics;
import java.awt.Graphics2D;
import java.awt.Image;
import java.awt.RenderingHints;
import java.awt.Toolkit;
import java.util.ArrayList;
public class ThreeDimension {
public static void main(String[] args) {
new DrawMain().drawMain();
}
}
class DrawMain {
// 描画領域
final int AREA_X = 500;
final int AREA_Y = 500;
// ウインドウサイズ
final int W_WIDTH = AREA_X + 16;
final int W_HEIGHT = AREA_Y + 39;
// JFrame
MyJFrame jf = new MyJFrame("疑似3D", W_WIDTH, W_HEIGHT);
// 描画用クラス
Graphics gr = jf.jp.bImg.createGraphics();
// 文字を綺麗に描画するために使用
Graphics2D g2 = (Graphics2D) gr;
// 画像枚数
final int IMG_NUM = 9;
// 画像
Image[] img = new Image[IMG_NUM];
// 色
Color WHITE = new Color(255, 255, 255);
Color BLACK = new Color(0, 0, 0);
Color CYAN = new Color(0, 255, 255);
// お題
ArrayList theme = new ArrayList<>();
DrawMain() {
// 画像の読込み
for (int i = 0; i < IMG_NUM; i++) {
img[i] = Toolkit.getDefaultToolkit()
.getImage("./img/m" + i + ".png");
}
// アンチエイリアス
g2.setRenderingHint(RenderingHints.KEY_TEXT_ANTIALIASING,
RenderingHints.VALUE_TEXT_ANTIALIAS_ON);
}
void drawMain() {
}
}
まず手始めに距離による大きさだけを再現していきましょう。画像を描画する座標は変えずに見た目の大きさだけ変えていきます。計算は先ほどの反比例です。距離が 5~0.05 までを定速でループさせます。奥行は z で横縦が x, y にします。x, y は今までの座標のように左上が(0, 0)とするのが考えやすいです。この(0, 0)は描画領域の(0, 0)とは違います。3D空間の座標系です。
ThreeDimension.java
void drawMain() {
// z だけ
double x, y, z = 5;
double speed = 0.05;
while (!jf.kb.isPressed(KeyEvent.VK_ENTER)) {
gr.setColor(BLACK);
gr.fillRect(0, 0, AREA_X, AREA_Y);
gr.drawImage(img[6], 100, 100, (int) (32 / z), (int) (32 / z), jf);
z = (z - speed < 0.05) ? 5 : z - speed;
drawSleep(33);
}
}
void releaseEnter() {
while (jf.kb.isPressed(KeyEvent.VK_ENTER)) {
drawSleep(33);
}
}
void drawSleep(long time) {
jf.jp.draw();
try {
Thread.sleep(time);
} catch (InterruptedException e) {
e.printStackTrace();
}
}
どうでしょう?楽しくなってきましたか?遠くにいるときはなかなか近づいてくるようにみえませんが近くに来たら一瞬で大きくなっていきます。これが距離による見た目の大きさです。
画像サイズ 32 を z で割っているだけです。z で割るので距離が0のときは計算できません。マイナスのときもおかしなことになるので z は常に正になるようにしてください。
近くに来たときに大きくなり過ぎると思ったら描画する距離を調整します。今は視点からほぼ0距離で描画しています。視点からの距離を 1 にすれば元の画像サイズの等倍までしか拡大されません。つまり距離が 1 より近くなったら描画しないようにします。

z = (z - 0.05 < 1) ? 5 : z - 0.05;こうですね。試してみてください。
せっかく3Dにするなら近くに迫ったときは大きく描画したいですから視点からの距離はあまり遠ざけないようにするか遠ざけるなら大きい画像を使うか元のサイズより拡大して使いたいところです。
次は x, y をランダムにして定速で近づいてくるようにしてみましょう。上に出現したら近づいてくるほど上に見えるようにします。下なら下、左右も同じです。
これを考えるには先ほどより明確に描画する範囲を決めなければなりません。
3D空間の一番奥と手前が2Dの座標のどこにくるかわからないと描画できません。
まず3D空間の大きさから決めていきましょう。これは(x, y, z)が(3, 3, 5)にしましょう。これはあくまで目安です。どの範囲を描画するかによって変わるのでそれほど意味はありません。
一番手前は x, y の大きさにします。2Dの描画領域にすっぽりはまる大きさというわけです。これが一番簡単でわかりやすいです。
一番奥は画面の中央にします。これも中央が一番計算しやすいです。距離が 5 ですから 描画領域の 1/5 の大きさで矩形を考えます。この 1/5 の矩形は手前の描画領域をそのまま奥まで平行移動したものです。奥へいくほど3D空間の x, y の範囲はより広く描画領域に入ってくるので一番奥では(x, y)=(15, 15)の範囲が視界に入ることになります。

3D空間での画像の x, y 座標は画像の中心にします。出現時に 0~3 のランダムにします。
ここでおもむろに3D空間の座標をずらします。x, y は画面の中央を(0, 0)にします。x は右でプラス、左でマイナスなのは変わりません。y も同じです。
距離が 1 のときを基準にしたいと思います。距離が 1 のときに(3, 3)の範囲が描画領域と同じになるようにします。このときの画像の大きさが3D空間で 1 になるようにします。
これで必要なものは揃いました。計算していきましょう。
描画の座標 dx はまず3D空間の中央が 0 ですから基準は AREA_X / 2 になります。ここに x を加算していきますが奥行によるずれも考慮します。
こういうときはわかりやすい値を決めて計算するのが無難です。x が左端にいるときは -1.5 です。距離が 1 のときに描画領域の左端にいてほしい。
となると描画領域の中央は 250 ですから左端なら -1.5 * ??? / 1 = -250 となる ??? を知りたい。中央が 0 なので左端は -250 です。この ??? は AREA_X / 3.0 です。
なぜそうなるのかというと、3D空間は(3, 3, 5)と決めたからです。3D空間の 3 は2D座標の AREA_X と同じ意味です。 AREA_X / 3.0 は3D空間で x が 1 動いたときの2D座標での動きです。割合の計算ですね。
一番奥の左端にいるときは -1.5 * AREA_X / 3.0 / 5 = -50 となります。一番奥ですから奥行は 5 です。そして2D座標の中央から -50 ですね。右端なら +50 になります。
この説明でわかってもらえるか不安ですが、3D空間の座標を2Dに変換しています。
コードにしていきます。
ThreeDimension.java
releaseEnter();
// x, y, z
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
z = 5;
while (!jf.kb.isPressed(KeyEvent.VK_ENTER)) {
gr.setColor(BLACK);
gr.fillRect(0, 0, AREA_X, AREA_Y);
int dx = (int) (AREA_X / 2 + x * AREA_X / 3.0 / z);
int dy = (int) (AREA_Y / 2 + y * AREA_Y / 3.0 / z);
int sx = (int) (AREA_X / 3.0 / z / 2.0);
int sy = (int) (AREA_Y / 3.0 / z / 2.0);
gr.drawImage(img[7], dx - sx, dy - sy, sx * 2, sy * 2, jf);
if (z - speed < 0.05) {
z = 5;
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
} else {
z -= speed;
}
drawSleep(33);
}
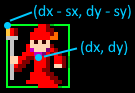
sx, sy は画像の描画するサイズの半分です。dx, dy は描画する画像の中心なので sx, sy を引いています。
画像サイズは距離が 1 のときに 1 になりますから3D空間の 1 は2Dだと AREA_X / 3.0 です。
どうでしょう?楽しめなくなってきましたか?
頭の中で1つ1つをしっかりイメージできればそれほど難しいわけではありません。描画する座標は中央を基準に x * 2Dの範囲 / 3Dの範囲 / z を加算しているだけです。
この「2Dの範囲 / 3Dの範囲 / z」で座標を変換しています。
とはいえ、私も久し振りに計算したので少し悩みました笑。
ここまでやっといてなんですが、疑似3Dはあまり使い道はありません!!!
というのも Java だと画像を動的に変形できないみたいなんですよね。変形とは元々矩形の画像を台形にしたり平行四辺形にしたりということです。DirectX ならそういう関数もありましたが Java は無いみたいです。静的に変形する方法はあるんですけどね。多分処理に時間がかかるので1フレームごとにたくさん変形させるゲームには使えません。ライブラリを探せばもしかしたら見つかるかもしれません。
変形できないと何が不便かというと、奥行のあるものはすべて変形するからです。
ここまでのコードでは奥行のある表現はしていますが画像に奥行はなく1枚の画像でしかありません。
例えば立方体を思い浮かべてください。今回のコードでは立方体の正面だけを描画したに過ぎません。側面を描画しようとすると縦横の揃った矩形では無理です。側面は視点によって形を変えますので事前に画像を用意することもできません。

といった理由で、それでも3Dを使いたいなら奥行を描画しないものにします。空とか宇宙なら地形などの奥行を表現しなくても大丈夫です。他には3Dダンジョンのように壁や床の位置が決まっているなら変形しなくても描画できるのであらかじめ変形している画像を何パターンか用意すればできると思います。2Dしかなかった昔のゲームでもそういった工夫をしています。
PHANTASY STAR は今でも続編が出たりしているようですが最初期は 1987年です。このゲームでダンジョンがぬるぬる動いているのを見て「すげーっ!」って興奮していましたね。おそらく今回のコードのような計算ではなく動いているところを全部画像にしたのではないかと思います。
工夫次第ではいけなくもないといった感じです。
ここまでのまとめ
見た目の大きさは奥行で割る
「2Dの範囲 / 3Dの範囲」で座標を変換
見た目の大きさは奥行で割る
「2Dの範囲 / 3Dの範囲」で座標を変換
画像を使わなければなんとか
ということで画像を使うといろいろ厄介な問題が多発するのでいっそのこと画像を使わないという発想をしてみます。
画像を使わなければ割と自由に3Dを表現できます。まずは線で立体を描画していきます。計算が簡単な正八面体にしましょう。正八面体は中心から x, y, z 方向に等距離の点を結んだ立体です。立体ですから奥行もあります。

先ほどのコードをコピペして画像ではなく12本の線を描画するように変更します。
立体の大きさは中心から ±0.5 のところに頂点があります。線を12本も描画するので計算量は多いですがそれぞれの頂点を先ほどの計算で2Dの座標に変換するだけです。
計算式をたくさん書くのは嫌なので中心からの距離 x, y, z について配列にしておきます。正八面体の頂点は6個です。頂点は vertex というらしいので vertexX, Y, Z です。
int型で頂点を2D座標に変換した値を格納する pos2DX, Y の配列も用意します。
どの点とどの点を結ぶのかも配列にしてしまいます。と思いましたが全部の点をつなげても15本なので全部つなげてしまいます。
まずは頂点の座標を全部2Dに変換してから線を描画していきます。
線を引くのは頂点の座標を総当たりしています。i が 0~4 まで、j は i+1~5 までです。2重ループですが同じところに線を引かないように i と j を決めています。総当たりも必要なときにすぐ書けるようにしておきたいところです。
立体には奥行があるので画像よりかえって3Dの雰囲気は出ているのではないでしょうか?ちょっとワクワクしませんか?これができればあとは頂点の位置を変えて線を結ぶだけでいろいろな形にできます。楽しくなってきますよね?
でもそれはそれで複雑な立体を作るには頂点の数が膨大になってしまうので大変なんですけどね。
ここまで動きが奥から手前の一直線だけですがシューティングで敵の動きを作ったときのように x, y, z の座標を変えていけばもっと楽しくなっていきます。
ですがまだちょっとした問題があります。実行するとわかると思いますが近づくにつれて手前側に伸びているように見えます。
これは距離が近すぎるからです。魚眼レンズのように近すぎると元の形が崩れてしまいます。これを解決するには視点からの距離を3くらいまで遠ざけます。遠くになるほど望遠レンズのように形そのままになります。遠ざけたので z の初期化も 20 くらいまで遠ざけます。距離が増えたので速度を 0.2 に増やします。
こうやってちょうどいいパラメータを見つけていきます。この調整ではまだ満足できません。距離が 3 までしか近付かないと描画領域の端に来る前に消えてしまいます。もう少し視野を狭くすることで画面全体を有意義に使えるように変更します。
これでだいぶ良くなりました。
ちょっとお遊びとして正八面体を回転させてみます。頂点の配列は[1]~[4]までが上右下左の順で入っているのでZ軸を中心に回転させます。
Z軸で回転させましたが他の軸でも同様にできます。X軸で回転するなら vertexY, Z を計算します。私は1軸だけの回転しか知りません。Unity では角度の計算に四元数を使うと知って軽く検索して「なんだこりゃ?」となって断念しました。四元数は複素数を使って3次元での角度を計算できるみたいです。
2軸以上の捻じれ回転もしくは四元数の計算方法を知っている人は教えてください。
次は線ではなくポリゴンを描画してみましょう。正八面体のコードをコピペして改変していきます。
正八面体は面を塗り潰すと前面の4つの三角形しか見えなくなります。今回は見えないところは無視して4つの三角形ポリゴンを描画します。
ループに入る前に必要なのは、どの頂点で三角形を作るかの配列、ポリゴンの頂点の x, y 配列、ポリゴンの x, y は3D座標ではなく2D座標です。それと一色の三角形が4つ集まっても四角にしか見えないので1つずつ色を変えるための配列も用意しておきましょう。
ポリゴンはまず Polygon クラスに x, y の配列と頂点数を渡してインスタンス化します。fillPoligon() にインスタンスを渡せば描画できます。今回は三角形ですが x, y の配列を増やせば複雑な多角形も描画できる…はずです。
線をポリゴンに変えているだけで他は変えていません。
ここまでできるとかなり夢が広がりますよね。あれもしたい、これもしたい、といった願望が出てくるのではないでしょうか。
しかしそんなに簡単なものでもありません。正八面体のような単純な立体ならまだどうにかなりますが少し複雑な形にするだけで難易度の高い問題がでてきます。
その1つがZソート問題です。Zは奥行のことです。ソートは並べ替えです。手前にくるほど後に描画するようにソートしなければなりません。
単純に距離が遠いものから描画していけば良いと考えてはいけません。1つの立方体でもZソートは必要です。立方体が右に見えるときは左の側面が見えますが、左に見えるときは右の側面が見えます。これは上下も同じです。上下の面を描画してから左右の面を描画すると上下の面が左右の面に浸食されます。
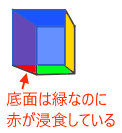
左右を先に描画しても同じ現象が発生します。
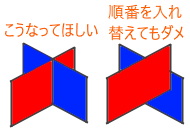
つまり毎回同じ順番で面を描画してはいないということです。見える位置によって描画順を変えなければなりません。これがZソートの難しいところです。立方体が回転していたら正面だった面が奥にいくかもしれません。どうやってソートするんでしょうね。面の重心がより手前でより中央なら後から描画するといった感じになるんですかね?私にはわかりません。
他にも面同士が交差したら両方の面を交差したところで切り取ってからZソートしないと必ずどちらかが浸食します。これはどうやって解決するんでしょうね。中途半端に交差してたらますます問題は難しくなります。
3D描画の計算を簡単なところだけやってきましたが一番可能性があるのは線画ですかね。画像やポリゴンは条件が揃わないと難しいです。
ということで線画をもう少し追加していきます。
床にタイルを敷き詰めたように線を描画します。これもこれまでに使った計算と同じです。3D空間内で線をどこからどこへ引けばいいのか座標を考えてそれを2Dに変換するだけです。
平坦な床ならZソート問題も気にしなくていいでのポリゴンでもいけますね。ポリゴンは一色なのでチェス盤のように色を互い違いにするのがいいでしょう。
強引に画像を使うとすればタイルの横1列を1つの画像にして手前に来るほど拡大させていきます。水平線が難しそうですが背景を重ねれば誤魔化せそうです。床は一色にして何かを床に置くことで床が動いているように見せる表現もあります。
これで視点の x, y をずらすとどう計算していけばいいでしょう?それをやったのが数年前に JavaScript で作ったゲームがこちら。
↓
DELINGER
ずらした2つの視点を平行法で見ると立体的に見えます。VRみたいなものですね。人間は右目と左目のずれから距離感を把握していますがそれを人為的に再現しています。
今コードを見てもどんな計算をしているのかさっぱりわかりません笑。試しながらごちゃごちゃ計算を追加していったのでそれっぽく動いていますが本来の計算とは異なっているかもしれません。
移動に合わせて視点も少しずれるようになっていますがまったくわかりません笑。
興味があればDELINGERのページで何もないところを右クリックして「ページのソースを表示」を選択してください。
ということで視点をずらしていきましょう。
目安として矩形を描画してキーボードで移動できるようにします。視点をずらすのが目的なのでここでは動ける範囲を決めないほうが視点の移動がわかりやすくなります。
矩形が上へ移動すると画面全体は下へ動くようにします。下へ移動したら画面は上へ、左右も同様に。
視点の移動では手前が大きくずれて奥は小さくずれますから z によってずれ幅が変わります。それは今までの計算と同じです。ただ矩形と逆方向へずれるのでマイナスにします。
ではコードにしていきましょう。先ほどのコードに追加・変更していきます。描画するものすべてに視点のずれを加算します。
操作があるのでまたキーコードと移動方向を配列にしています。
わかりやすくするために一番奥の面を矩形として描画します。
座標の計算はすべてずれを追加したので漏れがないようにしてください。唯一操作する矩形だけはずれを加算していません。同じ計算でずれを加算すると矩形は常に画面中央に留まることになります。
割り算の処理は足し算の数十倍だったかあるので AREA_X / 0.7 など何回も使う計算は先に定数にしておいてもいいかもしれません。
ここまでできればそれほど凝ったものはできないとしてもカジュアルな3Dゲームは作れると思います。
当たり判定はZ座標も加味して3D空間の座標で計算します。
3D空間を2Dの座標にできると3D空間内のものをマウスでクリックしたりもできます。画像でいうならその画像の描画サイズをクリック可能な範囲にすればいいですね。
また、座標の変換を反転して「3Dの範囲 / 2Dの範囲」とすれば逆の変換もできます。2Dには z の情報は含まれないので変換しても z は出てきません。その場合は奥行をどう考慮するか考えなければなりません。
3Dは工夫次第で何か面白いことができそうな可能性はありますが、冒頭で言ったように本格的に3Dをやりたいなら別の方法が近道です。
もし「ワイヤーフレームの表現がすごい好きで」といった人がいれば3Dの細かい計算を極めてもいいのではないでしょうか。
検索して出てくるのは行列(線形代数)なのですがコードとして有用なものは見つからなかったので複雑な行列を計算しました。その理屈を説明するのは今の私には無理ですが実装はできるようになりました。
全コードの後にそのコードも載せておきます。ポリゴンはZソートができないので線で描画した正八面体を3軸使って回転させています。
画像を使わなければ割と自由に3Dを表現できます。まずは線で立体を描画していきます。計算が簡単な正八面体にしましょう。正八面体は中心から x, y, z 方向に等距離の点を結んだ立体です。立体ですから奥行もあります。

先ほどのコードをコピペして画像ではなく12本の線を描画するように変更します。
立体の大きさは中心から ±0.5 のところに頂点があります。線を12本も描画するので計算量は多いですがそれぞれの頂点を先ほどの計算で2Dの座標に変換するだけです。
計算式をたくさん書くのは嫌なので中心からの距離 x, y, z について配列にしておきます。正八面体の頂点は6個です。頂点は vertex というらしいので vertexX, Y, Z です。
int型で頂点を2D座標に変換した値を格納する pos2DX, Y の配列も用意します。
どの点とどの点を結ぶのかも配列にしてしまいます。と思いましたが全部の点をつなげても15本なので全部つなげてしまいます。
まずは頂点の座標を全部2Dに変換してから線を描画していきます。
ThreeDimension.java
// 正八面体
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
z = 5;
// 頂点(中心からの距離)奥・上・右・下・左・手前の順
double[] vertexX = { 0, 0, 0.5, 0, -0.5, 0 };
double[] vertexY = { 0, -0.5, 0, 0.5, 0, 0 };
double[] vertexZ = { 0.5, 0, 0, 0, 0, -0.5 };
// 2D座標
int[] pos2DX = new int[6];
int[] pos2DY = new int[6];
while (!jf.kb.isPressed(KeyEvent.VK_ENTER)) {
gr.setColor(BLACK);
gr.fillRect(0, 0, AREA_X, AREA_Y);
// 頂点座標
for (int i = 0; i < vertexX.length; i++) {
pos2DX[i] = (int) (AREA_X / 2 + (x + vertexX[i]) *
AREA_X / 3.0 / (z + vertexZ[i]));
pos2DY[i] = (int) (AREA_Y / 2 + (y + vertexY[i]) *
AREA_Y / 3.0 / (z + vertexZ[i]));
}
gr.setColor(CYAN);
for (int i = 0; i < pos2DX.length - 1; i++) {
for (int j = i + 1; j < pos2DX.length; j++) {
gr.drawLine(pos2DX[i], pos2DY[i], pos2DX[j], pos2DY[j]);
}
}
if (z - speed < 0.5) {
z = 5;
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
} else {
z -= speed;
}
drawSleep(33);
}
座標の計算はコピペして正八面体の中心からの距離を足しているだけです。線を引くのは頂点の座標を総当たりしています。i が 0~4 まで、j は i+1~5 までです。2重ループですが同じところに線を引かないように i と j を決めています。総当たりも必要なときにすぐ書けるようにしておきたいところです。
立体には奥行があるので画像よりかえって3Dの雰囲気は出ているのではないでしょうか?ちょっとワクワクしませんか?これができればあとは頂点の位置を変えて線を結ぶだけでいろいろな形にできます。楽しくなってきますよね?
でもそれはそれで複雑な立体を作るには頂点の数が膨大になってしまうので大変なんですけどね。
ここまで動きが奥から手前の一直線だけですがシューティングで敵の動きを作ったときのように x, y, z の座標を変えていけばもっと楽しくなっていきます。
ですがまだちょっとした問題があります。実行するとわかると思いますが近づくにつれて手前側に伸びているように見えます。
これは距離が近すぎるからです。魚眼レンズのように近すぎると元の形が崩れてしまいます。これを解決するには視点からの距離を3くらいまで遠ざけます。遠くになるほど望遠レンズのように形そのままになります。遠ざけたので z の初期化も 20 くらいまで遠ざけます。距離が増えたので速度を 0.2 に増やします。
こうやってちょうどいいパラメータを見つけていきます。この調整ではまだ満足できません。距離が 3 までしか近付かないと描画領域の端に来る前に消えてしまいます。もう少し視野を狭くすることで画面全体を有意義に使えるように変更します。
ThreeDimension.java
z = 20;
speed = 0.2;
while (!jf.kb.isPressed(KeyEvent.VK_ENTER)) {
gr.setColor(BLACK);
gr.fillRect(0, 0, AREA_X, AREA_Y);
// 頂点座標
for (int i = 0; i < vertexX.length; i++) {
pos2DX[i] = (int) (AREA_X / 2 + (x + vertexX[i]) *
AREA_X / 0.7 / (z + vertexZ[i]));
pos2DY[i] = (int) (AREA_Y / 2 + (y + vertexY[i]) *
AREA_Y / 0.7 / (z + vertexZ[i]));
}
// ~略
if (z - speed < 3) {
z = 20;
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
視野を狭くするとは「2Dの範囲 / 3Dの範囲」を大きくすることです。3Dの範囲が狭くなれば大きく見えます。ここでは AREA_X / 0.7 にしました。これでだいぶ良くなりました。
ちょっとお遊びとして正八面体を回転させてみます。頂点の配列は[1]~[4]までが上右下左の順で入っているのでZ軸を中心に回転させます。
ThreeDimension.java
// 回転角
double rad = 0;
while (!jf.kb.isPressed(KeyEvent.VK_ENTER)) {
// ~略
for (int i = 1; i < 5; i++) {
vertexX[i] = Math.cos(rad + i * Math.PI / 2) * 0.5;
vertexY[i] = Math.sin(rad + i * Math.PI / 2) * 0.5;
}
rad += 0.1;
drawSleep(33);
}
for文で rad を基準に 90°ずつずらしています。簡単ですね。[0]と[5]はZ軸上にあるので回転しても変わりません。Z軸で回転させましたが他の軸でも同様にできます。X軸で回転するなら vertexY, Z を計算します。私は1軸だけの回転しか知りません。Unity では角度の計算に四元数を使うと知って軽く検索して「なんだこりゃ?」となって断念しました。四元数は複素数を使って3次元での角度を計算できるみたいです。
2軸以上の捻じれ回転もしくは四元数の計算方法を知っている人は教えてください。
次は線ではなくポリゴンを描画してみましょう。正八面体のコードをコピペして改変していきます。
正八面体は面を塗り潰すと前面の4つの三角形しか見えなくなります。今回は見えないところは無視して4つの三角形ポリゴンを描画します。
ループに入る前に必要なのは、どの頂点で三角形を作るかの配列、ポリゴンの頂点の x, y 配列、ポリゴンの x, y は3D座標ではなく2D座標です。それと一色の三角形が4つ集まっても四角にしか見えないので1つずつ色を変えるための配列も用意しておきましょう。
ポリゴンはまず Polygon クラスに x, y の配列と頂点数を渡してインスタンス化します。fillPoligon() にインスタンスを渡せば描画できます。今回は三角形ですが x, y の配列を増やせば複雑な多角形も描画できる…はずです。
ThreeDimension.java
releaseEnter();
// 正八面体をポリゴンで描画
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
z = 20;
// 正八面体の前面の4つの三角形の頂点のインデックス
int[][] triangle = { { 5, 1, 2 }, { 5, 2, 3 },
{ 5, 3, 4 }, { 5, 4, 1 } };
// ホリゴンの頂点座標
int[] px = new int[3];
int[] py = new int[3];
// ポリゴンの色
Color[] col = { new Color(255, 0, 0), new Color(255, 255, 0),
new Color(0, 255, 0), new Color(0, 0, 255) };
while (!jf.kb.isPressed(KeyEvent.VK_ENTER)) {
gr.setColor(BLACK);
gr.fillRect(0, 0, AREA_X, AREA_Y);
// 頂点座標
for (int i = 0; i < vertexX.length; i++) {
pos2DX[i] = (int) (AREA_X / 2 + (x + vertexX[i]) *
AREA_X / 0.7 / (z + vertexZ[i]));
pos2DY[i] = (int) (AREA_Y / 2 + (y + vertexY[i]) *
AREA_Y / 0.7 / (z + vertexZ[i]));
}
// 三角形の数だけループ
for (int i = 0; i < triangle.length; i++) {
// 三角形の頂点の数だけループ
for (int j = 0; j < triangle[0].length; j++) {
// 頂点の座標を代入
px[j] = pos2DX[triangle[i][j]];
py[j] = pos2DY[triangle[i][j]];
}
// ポリゴンインスタンス化
Polygon p = new Polygon(px, py, 3);
// ポリゴン描画
gr.setColor(col[i]);
gr.fillPolygon(p);
}
if (z - speed < 3) {
z = 20;
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
} else {
z -= speed;
}
for (int i = 1; i < 5; i++) {
vertexX[i] = Math.cos(rad + i * Math.PI / 2) * 0.5;
vertexY[i] = Math.sin(rad + i * Math.PI / 2) * 0.5;
}
rad += 0.1;
drawSleep(33);
}
ややこしいのは triangle[][] ですかね。これには pos2DX のインデックスが入っています。描画する三角形が4つでそれぞれの三角形の頂点が3つなので[4][3]の配列になっています。for文で i が 0 のときは pos2DX[5], [1], [2] の座標が px に代入されます。5, 1, 2 はそれぞれ手前、上、右の頂点です。その頂点を結んで三角形を描画します。線をポリゴンに変えているだけで他は変えていません。
ここまでできるとかなり夢が広がりますよね。あれもしたい、これもしたい、といった願望が出てくるのではないでしょうか。
しかしそんなに簡単なものでもありません。正八面体のような単純な立体ならまだどうにかなりますが少し複雑な形にするだけで難易度の高い問題がでてきます。
その1つがZソート問題です。Zは奥行のことです。ソートは並べ替えです。手前にくるほど後に描画するようにソートしなければなりません。
単純に距離が遠いものから描画していけば良いと考えてはいけません。1つの立方体でもZソートは必要です。立方体が右に見えるときは左の側面が見えますが、左に見えるときは右の側面が見えます。これは上下も同じです。上下の面を描画してから左右の面を描画すると上下の面が左右の面に浸食されます。

左右を先に描画しても同じ現象が発生します。
つまり毎回同じ順番で面を描画してはいないということです。見える位置によって描画順を変えなければなりません。これがZソートの難しいところです。立方体が回転していたら正面だった面が奥にいくかもしれません。どうやってソートするんでしょうね。面の重心がより手前でより中央なら後から描画するといった感じになるんですかね?私にはわかりません。
他にも面同士が交差したら両方の面を交差したところで切り取ってからZソートしないと必ずどちらかが浸食します。これはどうやって解決するんでしょうね。中途半端に交差してたらますます問題は難しくなります。

3D描画の計算を簡単なところだけやってきましたが一番可能性があるのは線画ですかね。画像やポリゴンは条件が揃わないと難しいです。
ということで線画をもう少し追加していきます。
床にタイルを敷き詰めたように線を描画します。これもこれまでに使った計算と同じです。3D空間内で線をどこからどこへ引けばいいのか座標を考えてそれを2Dに変換するだけです。
ThreeDimension.java
double distance = 0;
while (!jf.kb.isPressed(KeyEvent.VK_ENTER)) {
gr.setColor(BLACK);
gr.fillRect(0, 0, AREA_X, AREA_Y);
// 床のタイル
// 水平線
int ly0 = (int) (AREA_Y / 2 + 1.5 * AREA_Y / 0.7 / 20);
gr.setColor(CYAN);
gr.drawLine(0, ly0, AREA_X, ly0);
// 横線
for (int i = 5; i < 21; i++) {
int ly = (int) (AREA_Y / 2 + 1.5 * AREA_Y / 0.7 / (i + distance));
gr.drawLine(0, ly, AREA_X, ly);
}
// 縦線
for (int i = 0; i < 20; i++) {
int ly2 = (int) (AREA_Y / 2 + 1.5 * AREA_Y / 0.7 / 3);
int lx1 = (int) (AREA_X / 2 + (i - 10) * AREA_X / 1.0 / 20);
int lx2 = (int) (AREA_X / 2 + (i - 10) * AREA_X / 1.0 / 3);
gr.drawLine(lx1, ly0, lx2, ly2);
}
distance = (distance - 0.1 < -1) ? 0 : distance - 0.1;
distance で奥に向かってスクロールしているようにコントロールしています。縦線のスケールは若干変えて線20本がちょうど画面に入るように調整しています。平坦な床ならZソート問題も気にしなくていいでのポリゴンでもいけますね。ポリゴンは一色なのでチェス盤のように色を互い違いにするのがいいでしょう。
強引に画像を使うとすればタイルの横1列を1つの画像にして手前に来るほど拡大させていきます。水平線が難しそうですが背景を重ねれば誤魔化せそうです。床は一色にして何かを床に置くことで床が動いているように見せる表現もあります。
これで視点の x, y をずらすとどう計算していけばいいでしょう?それをやったのが数年前に JavaScript で作ったゲームがこちら。
↓
DELINGER
ずらした2つの視点を平行法で見ると立体的に見えます。VRみたいなものですね。人間は右目と左目のずれから距離感を把握していますがそれを人為的に再現しています。
今コードを見てもどんな計算をしているのかさっぱりわかりません笑。試しながらごちゃごちゃ計算を追加していったのでそれっぽく動いていますが本来の計算とは異なっているかもしれません。
移動に合わせて視点も少しずれるようになっていますがまったくわかりません笑。
興味があればDELINGERのページで何もないところを右クリックして「ページのソースを表示」を選択してください。
ということで視点をずらしていきましょう。
目安として矩形を描画してキーボードで移動できるようにします。視点をずらすのが目的なのでここでは動ける範囲を決めないほうが視点の移動がわかりやすくなります。
矩形が上へ移動すると画面全体は下へ動くようにします。下へ移動したら画面は上へ、左右も同様に。
視点の移動では手前が大きくずれて奥は小さくずれますから z によってずれ幅が変わります。それは今までの計算と同じです。ただ矩形と逆方向へずれるのでマイナスにします。
- AREA_X / 0.7 / zこれに矩形の座標を掛ければ矩形の座標によって視点がずれます。ずれ幅を調整するときは 0.7 を変えていきます。
ではコードにしていきましょう。先ほどのコードに追加・変更していきます。描画するものすべてに視点のずれを加算します。
操作があるのでまたキーコードと移動方向を配列にしています。
わかりやすくするために一番奥の面を矩形として描画します。
ThreeDimension.java
// 正八面体をポリゴンで描画
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
z = 20;
// 正八面体の前面の4つの三角形の頂点のインデックス
int[][] triangle = { { 5, 1, 2 }, { 5, 2, 3 },
{ 5, 3, 4 }, { 5, 4, 1 } };
// ホリゴンの頂点座標
int[] px = new int[3];
int[] py = new int[3];
// ポリゴンの色
Color[] col = { new Color(255, 0, 0), new Color(255, 255, 0),
new Color(0, 255, 0), new Color(0, 0, 255) };
double distance = 0;
// 四角座標
double sx = 0;
double sy = 0;
int[] kc = { KeyEvent.VK_UP, KeyEvent.VK_DOWN,
KeyEvent.VK_RIGHT, KeyEvent.VK_LEFT };
// 移動方向
double[] v = { 0, 0, 0.1, -0.1 };
double[] w = { -0.1, 0.1, 0, 0 };
while (!jf.kb.isPressed(KeyEvent.VK_ENTER)) {
gr.setColor(BLACK);
gr.fillRect(0, 0, AREA_X, AREA_Y);
// 床のタイル
int ly0 = (int) (AREA_Y / 2 - sy * AREA_Y / 0.7 / 20
+ 1.5 * AREA_Y / 0.7 / 20);
// 水平線
gr.setColor(CYAN);
gr.drawLine(0, ly0, AREA_X, ly0);
// 横線
for (int i = 5; i < 21; i++) {
int ly = (int) (AREA_Y / 2 - sy * AREA_Y / 0.7 / (i + distance)
+ 1.5 * AREA_Y / 0.7 / (i + distance));
gr.drawLine(0, ly, AREA_X, ly);
}
// 縦線
for (int i = 0; i < 20; i++) {
int ly2 = (int) (AREA_Y / 2 - sy * AREA_Y / 0.7 / 3
+ 1.5 * AREA_Y / 0.7 / 3);
int lx1 = (int) (AREA_X / 2 - sx * AREA_X / 0.7 / 20
+ (i - 10) * AREA_X / 1.0 / 20);
int lx2 = (int) (AREA_X / 2 - sx * AREA_X / 0.7 / 3
+ (i - 10) * AREA_X / 1.0 / 3);
gr.drawLine(lx1, ly0, lx2, ly2);
}
distance = (distance - 0.1 < -1) ? 0 : distance - 0.1;
// 一番奥の面
int lx1 = (int) (AREA_X / 2 - sx * AREA_X / 0.7 / 20
- 1.5 * AREA_X / 0.7 / 20);
int ly1 = (int) (AREA_Y / 2 - sy * AREA_Y / 0.7 / 20
- 1.5 * AREA_Y / 0.7 / 20);
gr.drawRect(lx1, ly1, (int) (3 * AREA_X / 0.7 / 20),
(int) (3 * AREA_Y / 0.7 / 20));
// 頂点座標
for (int i = 0; i < vertexX.length; i++) {
pos2DX[i] = (int) (AREA_X / 2
- sx * AREA_X / 0.7 / (z + vertexZ[i])
+ (x + vertexX[i]) * AREA_X / 0.7 / (z + vertexZ[i]));
pos2DY[i] = (int) (AREA_Y / 2
- sy * AREA_Y / 0.7 / (z + vertexZ[i])
+ (y + vertexY[i]) * AREA_Y / 0.7 / (z + vertexZ[i]));
}
// 三角形の数だけループ
for (int i = 0; i < triangle.length; i++) {
// 三角形の頂点の数だけループ
for (int j = 0; j < triangle[0].length; j++) {
// 頂点の座標を代入
px[j] = pos2DX[triangle[i][j]];
py[j] = pos2DY[triangle[i][j]];
}
// ポリゴンインスタンス化
Polygon p = new Polygon(px, py, 3);
// ポリゴン描画
gr.setColor(col[i]);
gr.fillPolygon(p);
}
// キー入力で移動
for (int i = 0; i < kc.length; i++) {
if (jf.kb.isPressed(kc[i])) {
sx += v[i];
sy += w[i];
}
}
// 操作する矩形
gr.setColor(CYAN);
gr.drawRect((int) (AREA_X / 2 + sx * AREA_X / 0.7 / 3 - 30),
(int) (AREA_Y / 2 + sy * AREA_Y / 0.7 / 3 - 30), 60, 60);
if (z - speed < 3) {
z = 20;
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
} else {
z -= speed;
}
for (int i = 1; i < 5; i++) {
vertexX[i] = Math.cos(rad + i * Math.PI / 2) * 0.5;
vertexY[i] = Math.sin(rad + i * Math.PI / 2) * 0.5;
}
rad += 0.1;
drawSleep(33);
}
どうでしょう?自由に動けると楽しくなってきますね。範囲を制限していないので床の下にも移動できます。床の下に移動すると床だったものが天井に見えます。座標の計算はすべてずれを追加したので漏れがないようにしてください。唯一操作する矩形だけはずれを加算していません。同じ計算でずれを加算すると矩形は常に画面中央に留まることになります。
割り算の処理は足し算の数十倍だったかあるので AREA_X / 0.7 など何回も使う計算は先に定数にしておいてもいいかもしれません。
ここまでできればそれほど凝ったものはできないとしてもカジュアルな3Dゲームは作れると思います。
当たり判定はZ座標も加味して3D空間の座標で計算します。
3D空間を2Dの座標にできると3D空間内のものをマウスでクリックしたりもできます。画像でいうならその画像の描画サイズをクリック可能な範囲にすればいいですね。
また、座標の変換を反転して「3Dの範囲 / 2Dの範囲」とすれば逆の変換もできます。2Dには z の情報は含まれないので変換しても z は出てきません。その場合は奥行をどう考慮するか考えなければなりません。
3Dは工夫次第で何か面白いことができそうな可能性はありますが、冒頭で言ったように本格的に3Dをやりたいなら別の方法が近道です。
もし「ワイヤーフレームの表現がすごい好きで」といった人がいれば3Dの細かい計算を極めてもいいのではないでしょうか。
ここまでのまとめ
頂点の2D座標が取得できれば線画もポリゴンもいける
ポリゴン描画にはZソートなどの難問もある
この記事を書いてから数日後に回転を極めようと勉強してみました。頂点の2D座標が取得できれば線画もポリゴンもいける
ポリゴン描画にはZソートなどの難問もある
検索して出てくるのは行列(線形代数)なのですがコードとして有用なものは見つからなかったので複雑な行列を計算しました。その理屈を説明するのは今の私には無理ですが実装はできるようになりました。
全コードの後にそのコードも載せておきます。ポリゴンはZソートができないので線で描画した正八面体を3軸使って回転させています。
ThreeDimensionクラスの全コード
ThreeDimension.java
package application;
import java.awt.Color;
import java.awt.Graphics;
import java.awt.Graphics2D;
import java.awt.Image;
import java.awt.Polygon;
import java.awt.RenderingHints;
import java.awt.Toolkit;
import java.awt.event.KeyEvent;
import java.util.ArrayList;
public class ThreeDimension {
public static void main(String[] args) {
new DrawMain().drawMain();
}
}
class DrawMain {
// 描画領域
final int AREA_X = 500;
final int AREA_Y = 500;
// ウインドウサイズ
final int W_WIDTH = AREA_X + 16;
final int W_HEIGHT = AREA_Y + 39;
// JFrame
MyJFrame jf = new MyJFrame("疑似3D", W_WIDTH, W_HEIGHT);
// 描画用クラス
Graphics gr = jf.jp.bImg.createGraphics();
// 文字を綺麗に描画するために使用
Graphics2D g2 = (Graphics2D) gr;
// 画像枚数
final int IMG_NUM = 9;
// 画像
Image[] img = new Image[IMG_NUM];
// 色
Color WHITE = new Color(255, 255, 255);
Color BLACK = new Color(0, 0, 0);
Color CYAN = new Color(0, 255, 255);
// お題
ArrayList theme = new ArrayList<>();
DrawMain() {
// 画像の読込み
for (int i = 0; i < IMG_NUM; i++) {
img[i] = Toolkit.getDefaultToolkit()
.getImage("./img/m" + i + ".png");
}
// アンチエイリアス
g2.setRenderingHint(RenderingHints.KEY_TEXT_ANTIALIASING,
RenderingHints.VALUE_TEXT_ANTIALIAS_ON);
}
void drawMain() {
// z だけ
double x, y, z = 5;
double speed = 0.05;
while (!jf.kb.isPressed(KeyEvent.VK_ENTER)) {
gr.setColor(BLACK);
gr.fillRect(0, 0, AREA_X, AREA_Y);
gr.drawImage(img[6], 100, 100, (int) (32 / z), (int) (32 / z), jf);
z = (z - 0.05 < 0.05) ? 5 : z - 0.05;
drawSleep(33);
}
releaseEnter();
// x, y, z
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
z = 5;
while (!jf.kb.isPressed(KeyEvent.VK_ENTER)) {
gr.setColor(BLACK);
gr.fillRect(0, 0, AREA_X, AREA_Y);
int dx = (int) (AREA_X / 2 + x * AREA_X / 3.0 / z);
int dy = (int) (AREA_Y / 2 + y * AREA_Y / 3.0 / z);
int sx = (int) (AREA_X / 3.0 / z / 2.0);
int sy = (int) (AREA_Y / 3.0 / z / 2.0);
gr.drawImage(img[7], dx - sx, dy - sy, sx * 2, sy * 2, jf);
if (z - speed < 0.05) {
z = 5;
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
} else {
z -= speed;
}
drawSleep(33);
}
releaseEnter();
// 正八面体
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
z = 20;
speed = 0.2;
// 頂点(中心からの距離)
double[] vertexX = { 0, 0, 0.5, 0, -0.5, 0 };
double[] vertexY = { 0, -0.5, 0, 0.5, 0, 0 };
double[] vertexZ = { 0.5, 0, 0, 0, 0, -0.5 };
// 2D座標
int[] pos2DX = new int[6];
int[] pos2DY = new int[6];
// 回転角
double rad = 0;
while (!jf.kb.isPressed(KeyEvent.VK_ENTER)) {
gr.setColor(BLACK);
gr.fillRect(0, 0, AREA_X, AREA_Y);
// 頂点座標
for (int i = 0; i < vertexX.length; i++) {
pos2DX[i] = (int) (AREA_X / 2 + (x + vertexX[i]) *
AREA_X / 0.7 / (z + vertexZ[i]));
pos2DY[i] = (int) (AREA_Y / 2 + (y + vertexY[i]) *
AREA_Y / 0.7 / (z + vertexZ[i]));
}
gr.setColor(CYAN);
for (int i = 0; i < pos2DX.length - 1; i++) {
for (int j = i + 1; j < pos2DX.length; j++) {
gr.drawLine(pos2DX[i], pos2DY[i], pos2DX[j], pos2DY[j]);
}
}
if (z - speed < 3) {
z = 20;
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
} else {
z -= speed;
}
for (int i = 1; i < 5; i++) {
vertexX[i] = Math.cos(rad + i * Math.PI / 2) * 0.5;
vertexY[i] = Math.sin(rad + i * Math.PI / 2) * 0.5;
}
rad += 0.1;
drawSleep(33);
}
releaseEnter();
// 正八面体をポリゴンで描画
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
z = 20;
// 正八面体の前面の4つの三角形の頂点のインデックス
int[][] triangle = { { 5, 1, 2 }, { 5, 2, 3 },
{ 5, 3, 4 }, { 5, 4, 1 } };
// ホリゴンの頂点座標
int[] px = new int[3];
int[] py = new int[3];
// ポリゴンの色
Color[] col = { new Color(255, 0, 0), new Color(255, 255, 0),
new Color(0, 255, 0), new Color(0, 0, 255) };
double distance = 0;
// 四角座標
double sx = 0;
double sy = 0;
int[] kc = { KeyEvent.VK_UP, KeyEvent.VK_DOWN,
KeyEvent.VK_RIGHT, KeyEvent.VK_LEFT };
// 移動方向
double[] v = { 0, 0, 0.1, -0.1 };
double[] w = { -0.1, 0.1, 0, 0 };
while (!jf.kb.isPressed(KeyEvent.VK_ENTER)) {
gr.setColor(BLACK);
gr.fillRect(0, 0, AREA_X, AREA_Y);
// 床のタイル
int ly0 = (int) (AREA_Y / 2 - sy * AREA_Y / 0.7 / 20
+ 1.5 * AREA_Y / 0.7 / 20);
// 水平線
gr.setColor(CYAN);
gr.drawLine(0, ly0, AREA_X, ly0);
// 横線
for (int i = 5; i < 21; i++) {
int ly = (int) (AREA_Y / 2 - sy * AREA_Y / 0.7 / (i + distance)
+ 1.5 * AREA_Y / 0.7 / (i + distance));
gr.drawLine(0, ly, AREA_X, ly);
}
// 縦線
for (int i = 0; i < 20; i++) {
int ly2 = (int) (AREA_Y / 2 - sy * AREA_Y / 0.7 / 3
+ 1.5 * AREA_Y / 0.7 / 3);
int lx1 = (int) (AREA_X / 2 - sx * AREA_X / 0.7 / 20
+ (i - 10) * AREA_X / 1.0 / 20);
int lx2 = (int) (AREA_X / 2 - sx * AREA_X / 0.7 / 3
+ (i - 10) * AREA_X / 1.0 / 3);
gr.drawLine(lx1, ly0, lx2, ly2);
}
distance = (distance - 0.1 < -1) ? 0 : distance - 0.1;
// 一番奥の面
int lx1 = (int) (AREA_X / 2 - sx * AREA_X / 0.7 / 20
- 1.5 * AREA_X / 0.7 / 20);
int ly1 = (int) (AREA_Y / 2 - sy * AREA_Y / 0.7 / 20
- 1.5 * AREA_Y / 0.7 / 20);
gr.drawRect(lx1, ly1, (int) (3 * AREA_X / 0.7 / 20),
(int) (3 * AREA_Y / 0.7 / 20));
// 頂点座標
for (int i = 0; i < vertexX.length; i++) {
pos2DX[i] = (int) (AREA_X / 2
- sx * AREA_X / 0.7 / (z + vertexZ[i])
+ (x + vertexX[i]) * AREA_X / 0.7 / (z + vertexZ[i]));
pos2DY[i] = (int) (AREA_Y / 2
- sy * AREA_Y / 0.7 / (z + vertexZ[i])
+ (y + vertexY[i]) * AREA_Y / 0.7 / (z + vertexZ[i]));
}
// 三角形の数だけループ
for (int i = 0; i < triangle.length; i++) {
// 三角形の頂点の数だけループ
for (int j = 0; j < triangle[0].length; j++) {
// 頂点の座標を代入
px[j] = pos2DX[triangle[i][j]];
py[j] = pos2DY[triangle[i][j]];
}
// ポリゴンインスタンス化
Polygon p = new Polygon(px, py, 3);
// ポリゴン描画
gr.setColor(col[i]);
gr.fillPolygon(p);
}
// キー入力で移動
for (int i = 0; i < kc.length; i++) {
if (jf.kb.isPressed(kc[i])) {
sx += v[i];
sy += w[i];
}
}
// 操作する矩形
gr.setColor(CYAN);
gr.drawRect((int) (AREA_X / 2 + sx * AREA_X / 0.7 / 3 - 30),
(int) (AREA_Y / 2 + sy * AREA_Y / 0.7 / 3 - 30), 60, 60);
if (z - speed < 3) {
z = 20;
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
} else {
z -= speed;
}
for (int i = 1; i < 5; i++) {
vertexX[i] = Math.cos(rad + i * Math.PI / 2) * 0.5;
vertexY[i] = Math.sin(rad + i * Math.PI / 2) * 0.5;
}
rad += 0.1;
drawSleep(33);
}
}
void releaseEnter() {
while (jf.kb.isPressed(KeyEvent.VK_ENTER)) {
drawSleep(33);
}
}
void drawSleep(long time) {
jf.jp.draw();
try {
Thread.sleep(time);
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}
ThreeDimension.java
// 正八面体
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
z = 20;
speed = 0.2;
// 頂点(中心からの距離)
double[] vertexX = { 0, 0, 1, 0, -1, 0 };
double[] vertexY = { 0, -1, 0, 1, 0, 0 };
double[] vertexZ = { 1, 0, 0, 0, 0, -1 };
// 2D座標
int[] pos2DX = new int[6];
int[] pos2DY = new int[6];
// 回転角
double rad = 0.1;
double rad2 = 0.05;
double rad3 = 0.03;
while (!jf.kb.isPressed(KeyEvent.VK_ENTER)) {
gr.setColor(BLACK);
gr.fillRect(0, 0, AREA_X, AREA_Y);
// 頂点座標
for (int i = 0; i < vertexX.length; i++) {
pos2DX[i] = (int) (AREA_X / 2 + (x + vertexX[i]) *
AREA_X / 0.7 / (z + vertexZ[i]));
pos2DY[i] = (int) (AREA_Y / 2 + (y + vertexY[i]) *
AREA_Y / 0.7 / (z + vertexZ[i]));
}
gr.setColor(CYAN);
for (int i = 0; i < pos2DX.length - 1; i++) {
for (int j = i + 1; j < pos2DX.length; j++) {
gr.drawLine(pos2DX[i], pos2DY[i], pos2DX[j], pos2DY[j]);
}
}
if (z - speed < 3) {
z = 20;
x = Math.random() * 3 - 1.5;
y = Math.random() * 3 - 1.5;
} else {
z -= speed;
}
// 3軸回転
for (int i = 0; i < 6; i++) {
double X = vertexX[i];
double Y = vertexY[i];
double Z = vertexZ[i];
double s1 = Math.sin(rad);
double s2 = Math.sin(rad2);
double s3 = Math.sin(rad3);
double c1 = Math.cos(rad);
double c2 = Math.cos(rad2);
double c3 = Math.cos(rad3);
vertexX[i] = c2 * c3 * X
+ c2 * -s3 * Y
+ s2 * Z;
vertexY[i] = (-s1 * -s2 * c3 + c1 * s3) * X
+ (-s1 * -s2 * -s3 + c1 * c3) * Y +
-s1 * c2 * Z;
vertexZ[i] = (c1 * -s2 * c3 + s1 * s3) * X
+ (c1 * -s2 * -s3 + s1 * c3) * Y
+ c1 * c2 * Z;
}
drawSleep(33);
}
releaseEnter();
このコードは正八面体を線で描画するコードを書き換えたものです。そのまま追加しようとすると変数の宣言がダブったりします。
かなりえぐい式ですよね。2次元の計算から1次元増えるだけでこれだけ複雑になります。式の見た目くらいは単純にするために短い変数名に代入しています。面白いのはXならXの座標を決めるのに X, Y, Z の3つとも必要になるところです。クォータービューでも似たようなことがありましたね。
この処理では1フレームごとに rad, rad2, rad3 を加算する必要はありません。現在の3D空間の座標からそれぞれの軸に合わせた角度だけ回転するようになっています。絶対的な角度ではなく現在の角度からの相対的な角度ということですね。1フレームごとに加算すると回転が加速していきます。
3×3 の行列が X, Y, Z軸の3つあってそれと X, Y, Z のベクトルとの行列積でコードのような式に展開できます。Xだけ計算が少ないのは行列の計算する順番によります。
私もこの式の具体的な説明はできないので「実装するならこんな計算が必要なのかあ…」くらいに思ってもらえればいいと思います。
きちんと3軸で回転しているか確かめるには rad(X軸), rad2(Y軸), rad3(Z軸) の1つだけに値を与えて他は 0 にします。X軸だけ値を与えればX軸で回転している様子を見ることができます。
これこれはアフィン変換というものです。アフィン変換では回転だけではなく平行移動や大きさの倍率も扱えます。
かなりえぐい式ですよね。2次元の計算から1次元増えるだけでこれだけ複雑になります。式の見た目くらいは単純にするために短い変数名に代入しています。面白いのはXならXの座標を決めるのに X, Y, Z の3つとも必要になるところです。クォータービューでも似たようなことがありましたね。
この処理では1フレームごとに rad, rad2, rad3 を加算する必要はありません。現在の3D空間の座標からそれぞれの軸に合わせた角度だけ回転するようになっています。絶対的な角度ではなく現在の角度からの相対的な角度ということですね。1フレームごとに加算すると回転が加速していきます。
3×3 の行列が X, Y, Z軸の3つあってそれと X, Y, Z のベクトルとの行列積でコードのような式に展開できます。Xだけ計算が少ないのは行列の計算する順番によります。
私もこの式の具体的な説明はできないので「実装するならこんな計算が必要なのかあ…」くらいに思ってもらえればいいと思います。
きちんと3軸で回転しているか確かめるには rad(X軸), rad2(Y軸), rad3(Z軸) の1つだけに値を与えて他は 0 にします。X軸だけ値を与えればX軸で回転している様子を見ることができます。
これこれはアフィン変換というものです。アフィン変換では回転だけではなく平行移動や大きさの倍率も扱えます。